Dense vs. Sparse Matrix Storage in FEM - A Wind Turbine Foundation Case Study
In structural engineering, finite element models use matrices to represent the stiffness of a system and solve for displacements. Each row (and column) in these matrices corresponds to a degree of freedom (DOF) of the structure. As the mesh is refined, the number of degrees of freedom increases, and the size of the stiffness matrix grows with the square of the number of DOFs.
These matrices are inherently sparse (mostly zeros due to localized element connectivity), but engineers choose how to store them computationally. Dense storage naively retains all entries (including zeros), while sparse storage compresses them. The choice drastically impacts memory and performance.
Why to use sparse storage?
The truth is that I only started to dig into sparse matrix storage after hitting a wall while developing my own FEM library.
In typical civil or building structures modeled with beam elements, memory wasn't a major issue, and so my implementation simply assembled the full stiffness matrix. It worked just fine.
However, when I switched to solid elements to more accurately model continuous systems, the size of the stiffness matrix exploded.
As I tested several medium-sized models with around 10,000 nodes, my computer would run out of memory and crash. After some inspections, I found out that the stiffness matrix would become enourmous quickly.
I wondered how could it be possible. I could solve systems with hundreds of thousands of nodes in the very same computer with commercial software like ANSYS.
The difference? Sparse matrix storage.
Most of the entries in the stiffness matrix where "irrelevant" zeros. Sparse matrix storage discards these, retaining only non-zero values and their locations.
After updating the solver to work with sparse matrices, my FEM library could store those in memory models with hundreds of thousands of nodes as effortlessly as commercial software.
How much memory is needed to store the stiffness matrix?
Let's estimate the memory requirements for storing the stiffness matrix in both dense and sparse storage formats.
Dense Matrix Storage
In a dense matrix implementation, you store every entry. If you have n degrees of freedom, you'll have a matrix size of n x n, resulting in n² float numbers stored in memory. If you store every entry as an 8-byte (double-precision) float, the total memory required is:
dense_matrix_memory = n * n * 8
For example, a model with 106k DOFs required 83.90 GB of memory.
Sparse Matrix Storage
Since most stiffness matrix entries are zero, we can store only the nonzero entries along with their row and column indices. Assuming each nonzero element requires storage for two 4-byte integers and one 8-byte float, the memory per nonzero is:
non_zero_element = 2 * 4 bytes + 1 * 8 bytes = 16 bytes
Even though each stored entry takes more bytes than a single dense storage entry (there's an overhead per non-zero value), the number of zeros will be orders of magnitude larger for most cases, making sparse matrix storage much more efficient.
For the same example of 106k DOFs, with a sparse matrix storage it only required 40 MB.
Onshore WTG Foundation Stiffness Matrix
Now, let's apply these concepts to a real example of an onshore wind turbine foundation.
We modelled the WTG foundation using solid elements and proposing different mesh configurations.
WTG Foundation - Coarse Mesh
The first iteration was with a very coarse mesh, resulting in very low memory requirements:
- Elements: 24
- Nodes: 110
- Degrees of freedom: 330
- Dense matrix storage: 0.8 MB
- Sparse matrix storage: 0.1 MB
At this point, the model was small enough to make the memory requirements negligible for both dense and sparse matrix formats.
However, this model was clearly unsuitable for any engineering study, both in terms of plan view shape (originally round) and section detail.
WTG Foundation - Mid-Dense Mesh
As we made the mesh denser, we quickly run out of memory when using dense matrix storage, as shown in this example:
- Elements: 8k
- Nodes: 35k
- Degrees of freedom: 106k
- Dense matrix storage: 83.90 GB
- Sparse matrix storage: 0.04 GB

Although the mesh could still be further refined, this model was already suitable analyses. However, using a dense matrix storage was imposible in our computer, while sparse storage remained absolutely manageable.
WTG Foundation - Dense Mesh
The last iteration we proposed was with a much denser mesh:
- Elements: 66k
- Nodes: 268k
- Degrees of freedom: 803k
- Dense matrix storage: 4,801.8 GB
- Sparse matrix storage: 0.3 GB

For this fine mesh model, dense storage was infeasible even for most workstations, requiring data center-level resources. Sparse storage, however, reduced memory demands by orders of magnitude, making the model (at just 0.3 GB) easily storable even on a low-end smartphone.
WTG Foundation - Mesh Comparison Summary
The following table contains a summary of a few of the meshes proposed for the study of this wind turbine foundation:
| Elements | Nodes | DOF | Non-zero Entries | Dense [GB] | Sparse [GB] |
|---|---|---|---|---|---|
| 24 | 110 | 330 | 9594 | 0.0008 | 0.0001 |
| 700 | 2,970 | 8,910 | 304,182 | 0.5915 | 0.0034 |
| 8,604 | 35,372 | 106,116 | 3,751,344 | 83.90 | 0.04 |
| 66,008 | 267,600 | 802,800 | 28,643,904 | 4,801.8 | 0.3 |
This video shows the evolution of number of elements and memory usage for both dense and sparse matrix storages, along with the evolution of the mesh of the WTG foundation.
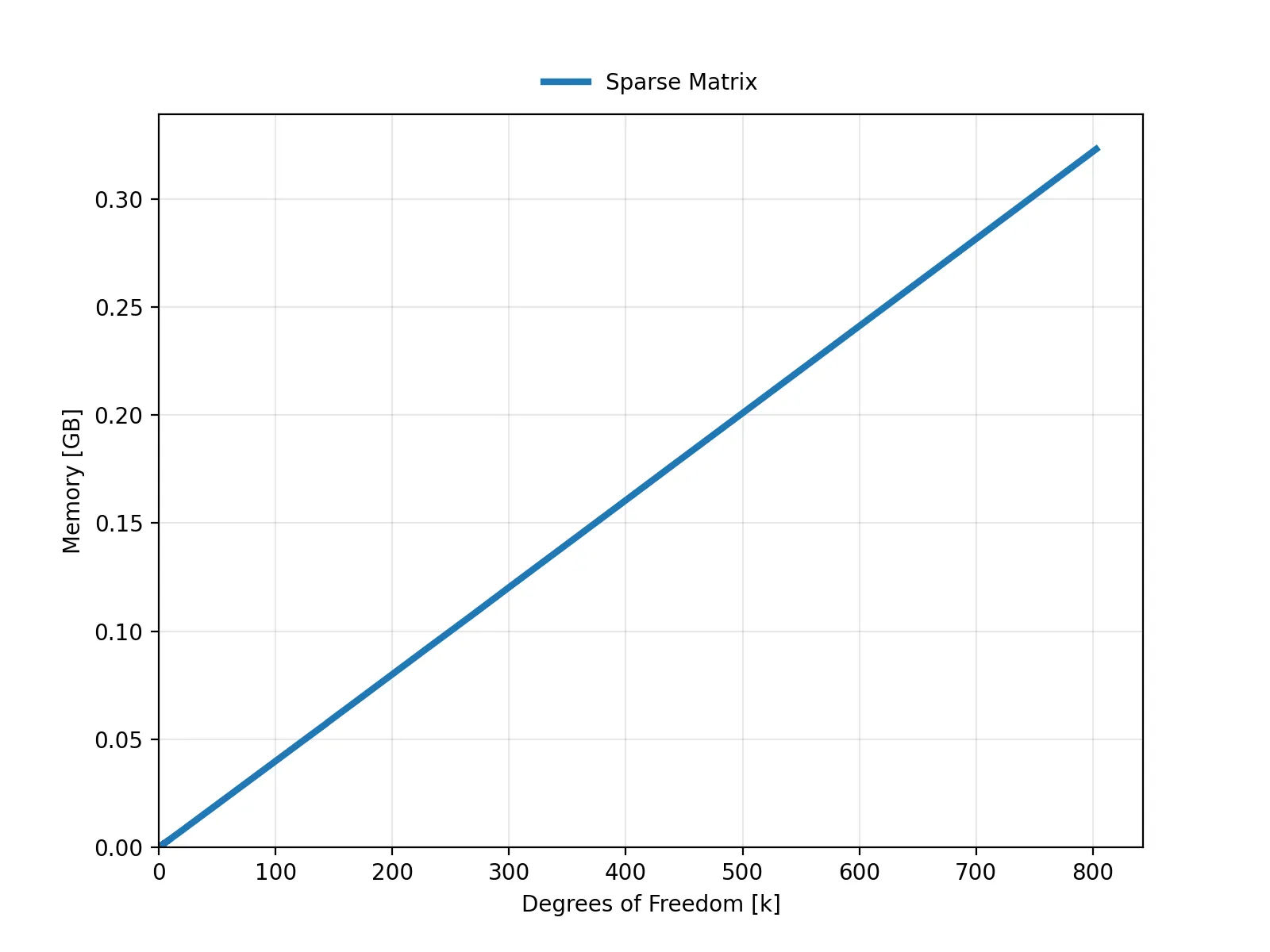
The previous animation shows the quadratic growth of the dense matrix storage, while the sparse's memory usage remains nearly flat, almost indistinguishable from the x-axis. When isolating the sparse's memory dependency on degrees of freedom, we see that the relationship is clearly linear.